Multiple scan data association by convex variational inference

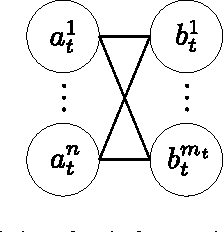
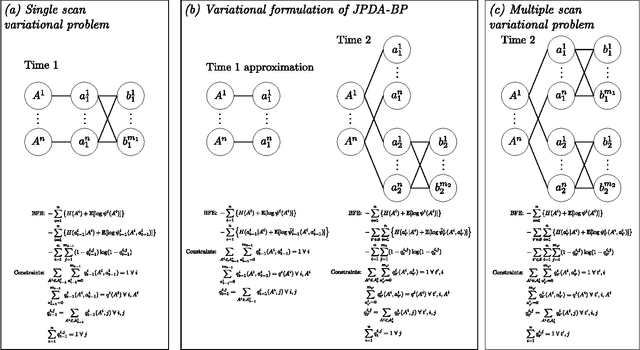
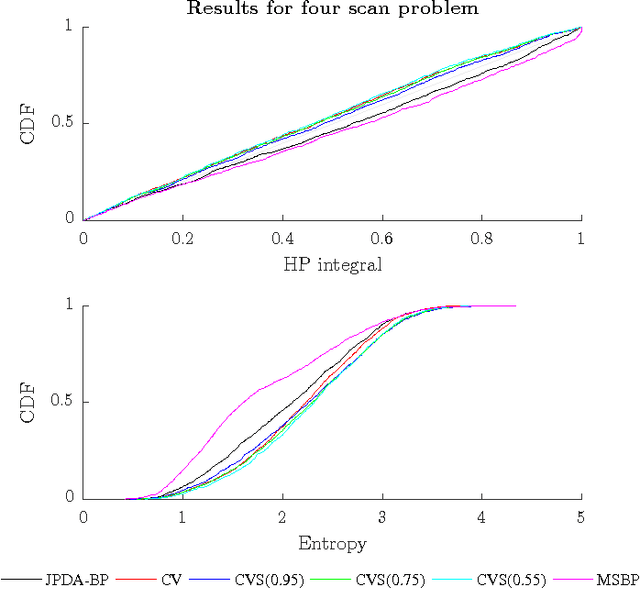
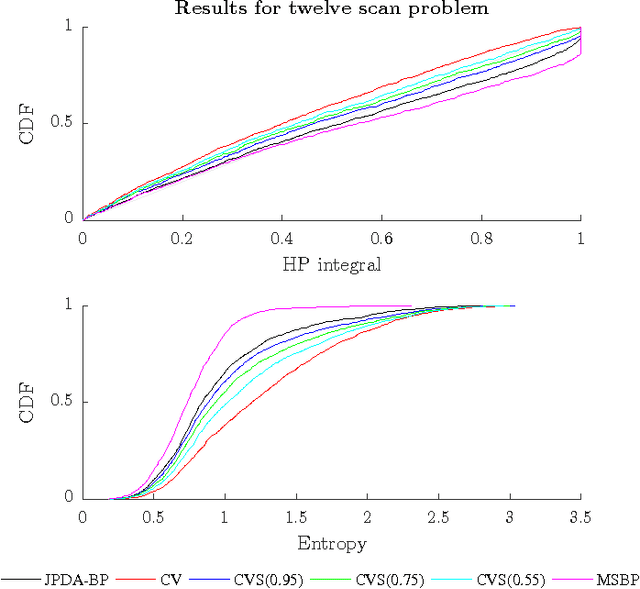
Data association, the reasoning over correspondence between targets and measurements, is a problem of fundamental importance in target tracking. Recently, belief propagation (BP) has emerged as a promising method for estimating the marginal probabilities of measurement to target association, providing fast, accurate estimates. The excellent performance of BP in the particular formulation used may be attributed to the convexity of the underlying free energy which it implicitly optimises. This paper studies multiple scan data association problems, i.e., problems that reason over correspondence between targets and several sets of measurements, which may correspond to different sensors or different time steps. We find that the multiple scan extension of the single scan BP formulation is non-convex and demonstrate the undesirable behaviour that can result. A convex free energy is constructed using the recently proposed fractional free energy (FFE). A convergent, BP-like algorithm is provided for the single scan FFE, and employed in optimising the multiple scan free energy using primal-dual coordinate ascent. Finally, based on a variational interpretation of joint probabilistic data association (JPDA), we develop a sequential variant of the algorithm that is similar to JPDA, but retains consistency constraints from prior scans. The performance of the proposed methods is demonstrated on a bearings only target localisation problem.

Approximate evaluation of marginal association probabilities with belief propagation

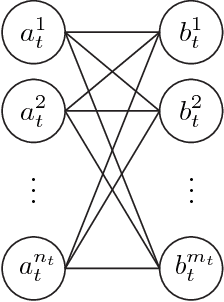
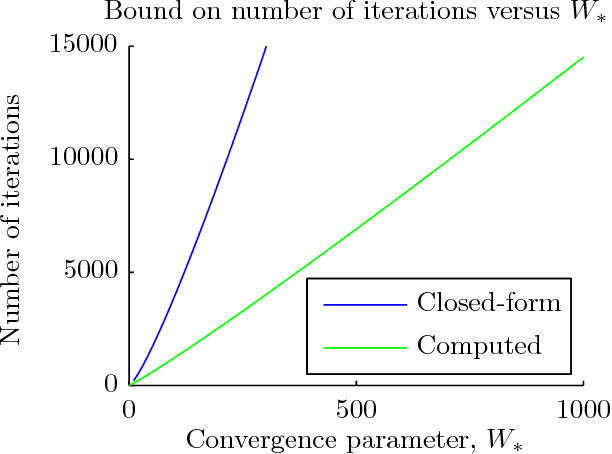
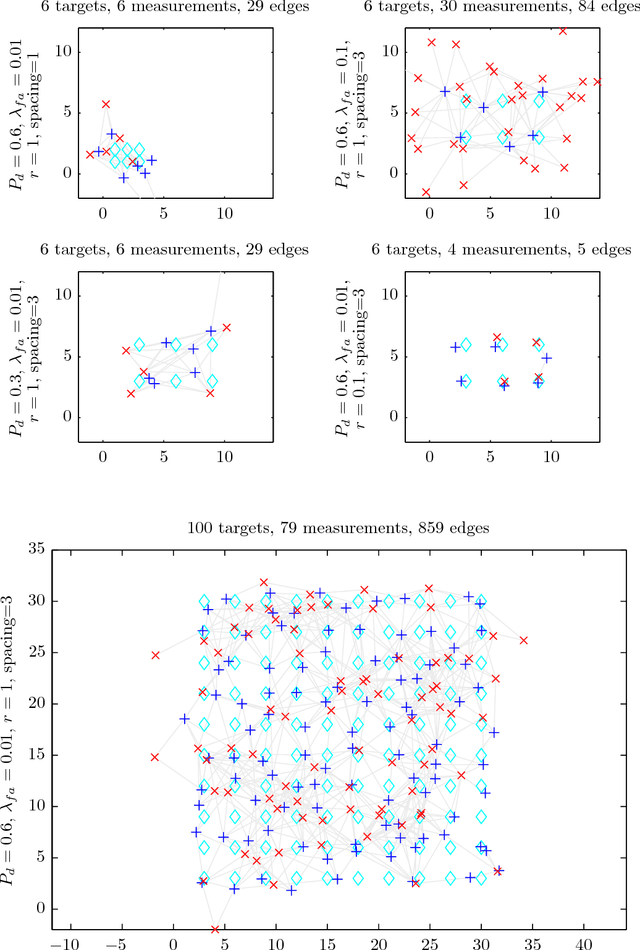
Data association, the problem of reasoning over correspondence between targets and measurements, is a fundamental problem in tracking. This paper presents a graphical model formulation of data association and applies an approximate inference method, belief propagation (BP), to obtain estimates of marginal association probabilities. We prove that BP is guaranteed to converge, and bound the number of iterations necessary. Experiments reveal a favourable comparison to prior methods in terms of accuracy and computational complexity.